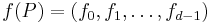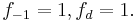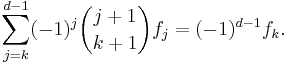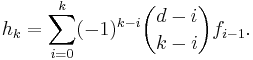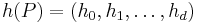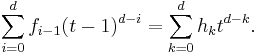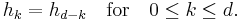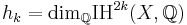Dehn–Sommerville equations

In mathematics, the Dehn–Sommerville equations are a complete set of linear relations between the numbers of faces of different dimension of a simplicial polytope. For polytopes of dimension 4 and 5, they were found by Max Dehn in 1905. Their general form was established by Duncan Sommerville in 1927. The Dehn–Sommerville equations can be restated as a symmetry condition for the h-vector of the simplicial polytope and this has become the standard formulation in recent combinatorics literature. By duality, analogous equations hold for simple polytopes.

Statement

Let P be a d-dimensional simplicial polytope. For i = 0, 1, ..., d−1, let fi denote the number of i-dimensional faces of P. The sequence

f(P)=(f_0,f_1,\ldots,f_{d-1})

is called the f-vector of the polytope P. Additionally, set

f_{-1}=1, f_d=1.

Then for any k = −1, 0, …, d−2, the following Dehn–Sommerville equation holds:

\sum_{j=k}^{d-1} (-1)^{j} \binom{j%2B1}{k%2B1} f_j = (-1)^{d-1}f_k.

When k = −1, it expresses the fact that Euler characteristic of a (d − 1)-dimensional simplicial sphere is equal to 1 + (−1)d−1.

Dehn–Sommerville equations with different k are not independent. There are several ways to choose a maximal independent subset consisting of \left[\frac{d%2B1}{2}\right] equations. If d is even then the equations with k = 0, 2, 4, …, d−2 are independent. Another independent set consists of the equations with k = −1, 1, 3, …, d−3. If d is odd then the equations with k = −1, 1, 3, …, d−2 form one independent set and the equations with k = −1, 0, 2, 4, …, d−3 form another.

Equivalent formulations

Main article: h-vector

Sommerville found a different way to state these equations:

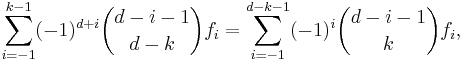
\sum_{i=-1}^{k-1}(-1)^{d%2Bi}\binom{d-i-1}{d-k} f_i = \sum_{i=-1}^{d-k-1}(-1)^{i}\binom{d-i-1}{k} f_i,

where 0 ≤ k ≤ ½(d−1). This can be further facilitated introducing the notion of h-vector of P. For k = 0, 1, …, d, let

h_k = \sum_{i=0}^k (-1)^{k-i}\binom{d-i}{k-i}f_{i-1}.

The sequence

h(P)=(h_0,h_1,\ldots,h_d)

is called the h-vector of P. The f-vector and the h-vector uniquely determine each other through the relation

\sum_{i=0}^{d}f_{i-1}(t-1)^{d-i}=\sum_{k=0}^{d}h_{k}t^{d-k}.

Then the Dehn–Sommerville equations can be restated simply as

h_k = h_{d-k} \quad\textrm{for}\quad 0\leq k\leq d.

The equations with 0 ≤ k ≤ ½(d−1) are independent, and the others are manifestly equivalent to them.

Richard Stanley gave an interpretation of the components of the h-vector of a simplicial convex polytope P in terms of the projective toric variety X associated with (the dual of) P. Namely, they are the dimensions of the even intersection cohomology groups of X:

h_k=\operatorname{dim}_{\mathbb{Q}}\operatorname{IH}^{2k}(X,\mathbb{Q})

(the odd intersection cohomology groups of X are all zero). In this language, the last form of the Dehn–Sommerville equations, the symmetry of the h-vector, is a manifestation of the Poincaré duality in the intersection cohomology of X.

References